



Figure 1: Example Equations
Using TeX (pronounced tek) markup to typeset equations has three huge advantages over the many GUI apps out there:
"But," I hear you ask, "isn't the cryptic markup of TeX old-school? Isn't it easier to just use a GUI application for typesetting equations? You would think so, wouldn't you? The night I got a take-home exam in my first graduate-level statistics seminar, I found myself in immediate need for something to quickly produce good looking equations. So naturally I tried out a few of the GUI apps like MathType, MathMagic and Mac OS X's Grapher. After about five hours experimenting with them I still couldn't figure out how to make any of them do seemingly simple things. And I found them all extremely clunky when trying to modify equations. They would constantly do things I didn't intend.
Now, having been a computer geek since 1984 I had always been aware of Donald Knuth's TeX typesetting system for scientific papers, so I thought maybe I should finally give TeX a try. Within 20 minutes of opening a little Mac app called LaTeXiT (and with help from a this nice TeX math cheat sheet) I was turning to random pages in my stats book and easily typesetting any equation on the page! (See Figure 1.) It really is that easy. I ended up typesetting my entire exam with LaTeX (pronounced LAY-tek, an extension of TeX), just as an exercise to finally learn how to use it (and it was not so easy). But you don't have to learn how to typeset your entire papers with LaTeX just to use it for equations.
In this article I'll start with a short interactive tutorial so that you can experience just how easy it really is to typeset equations with TeX markup. Then I'll show you how you can put these equations into word processing and presentation applications, and even onto Web pages.
This short interactive tutorial will introduce markup codes and concepts one step at a time, and allow you try them out as you go. Enter the syntax in the text box at the bottom of the tutorial area and you'll see it typeset in the middle box whenever you click the "TYPESET IT" button. Just click the "Next" button to move to the next step, or click the small boxes to go to any specific step.
Let's begin with a very small equation, a simple linear model. In the text box at the bottom (the "input" box), type "y = a + bx" (without the quotes), then click the "TYPESET IT" button. You should see the following show up in the middle box (the "output" box):
$$ y = a + bx $$
TeX uses very simple markup codes for special characters
and functions. The codes begin with a backslash \ followed by a
word that describes the character or function.
For example, try typesetting
this: "y = \alpha + \beta x + \epsilon". (Note the space between
\beta and x. You need that because there's no code named "\betax". It's
important to know that the spaces you type will not be included in
the typeset equation, because TeX controls all the spacing within
equations.) This is what you should see:
$$ y = \alpha + \beta x + \epsilon $$
Here are a few more codes for you to try. Note that some codes begin with an UPPERCASE letter. Try those with that first letter in lowercase and see what you get.
| \(\mu\) | – \mu | \(\gamma\) | – \gamma | \(\Delta\) | – \Delta | \(\lbrace\) | – \lbrace |
| \(\pm\) | – \pm | \(\div\) | – \div | \(\times\) | – \times | \(\approx\) | – \approx |
| \(\in\) | – \in | \(\geq\) | – \geq | \(\prime\) | – \prime | \(\Rightarrow\) | – \Rightarrow |
You can find a complete list in Short Math Guide for LaTeX. You'll need to take the time to look through that after this tutorial.
TeX uses braces, { and }, to enclose sequences of
characters that should to be taken together and treated as a whole phrase.
So, for example, if you wanted to make the fraction \(\frac 1 2\) you could
just type "\frac 1 2" (try that now). But if you need to put more than just
a single character in the numerator or denominator, you need to enclose them
in braces.
So try this: "z = \frac {x - \mu} \sigma" and you should get this:
$$ z = \frac {x - \mu} \sigma $$
Diacritic marks are produced with a code for the mark followed by a space (remember, spaces are ignored), then the letter that the mark should appear over. Some marks can span across several letters, in which case the letters must be enclosed in braces. Try these:
| \(\breve x\) | – \breve x | \(\dot x\) | – \dot x | \(\hat x\) | – \hat x | \(\widehat{xxx}\) | – \widehat{xxx} |
| \(\check x\) | – \check x | \(\ddot x\) | – \ddot x | \(\bar x\) | – \bar x | \(\overline{xxx}\) | – \overline{xxx} |
| \(\vec x\) | – \vec x | \(\dddot x\) | – \dddot x | \(\tilde x\) | – \tilde x | \(\widetilde{xxx}\) | – \widetilde{xxx} |
Superscripts and subscripts are
specified with the ^ and _ symbols, respectively, followed by the
single character that should be superscripted or subscripted.
Try this: "\sum (x_i - \bar x)^2", and you should get this:
$$ \sum (x_i - \bar x)^2 $$
It's important to understand that the superscript or subscript is only applied to the first single character after the ^ or _ symbol. (As we'll see, that's the case for many codes in TeX.) If you need to superscript or subscript a number with more than one digit, or a negative number, or even a whole mathematical phrase, you must enclose it in braces.
So try typing "p_12" and see what happens. In order for the 1 and
2 to be treated as a single unit, just enclose them in braces, like
this: "p_{12}". You should see \(p_{12}\)
Then try: "e ^ {-(b_0 + b_1 X_1 + \epsilon_i)}". You should see \(e ^ {-(b_0 + b_1 X_1 + \epsilon_i)}\).
Now what if you need a variable to have both a superscript and a subscript? It's actually quite easy. If you follow a variable with both a superscript and a subscript, TeX assumes you meant for both of them to be applied to that variable. For example, try typing "x _ \mu ^ 2". You should see \(x _ \mu ^ 2\). It doesn't matter what order you put them in, "x ^ 2 _ \mu" will work the same. But if, say, the subscript also needs a subscript, you'll need to use braces, as such: "x _ {\mu_1} ^ 2", which should give you \(x _ {\mu_1} ^ 2\). Try it and experiment with it a bit.
TeX treats superscripts and subscripts in a special way when they are applied to the sumation \(\Sigma\) or integral \(\int\) symbols. In these special cases they are treated as the limits for those symbols, so the superscript is placed on top and the subscript is placed underneath the symbol. (Sometimes, depending on the context, TeX will put them beside the symbol rather than on the top and bottom. So don't think you made a mistake.) Try this: "\sum ^ n _ {i=1}":
$$ \sum ^ n _ {i=1} $$
You can place any arbitrary superscript-sized symbol above or below any other symbol by using the \overset and \underset codes. These codes, like \frac, take two sets of braces. The first contains the symbols to place above or below the symbols within the second braces. So, for example, typeset "\overset n X " or "\underset {n-1} X" and you should get one of the following, respectively:
$$ \overset n X \quad \underset {n-1} X $$
If you need to force some extra space, you can use one of the following (the thin ones don't show up so well on Web pages):
| \(x \, y\) | \, (thin space) |
| \(x \: y\) | \: (medium space) |
| \(x \; y\) | \; (thick space) |
| \(x \quad y\) | \quad |
| \(x \qquad y\) | \qquad |
You may have noticed that TeX automatically italicizes all letters, assuming that they are variables. For named operators such as log() or sin(), TeX has many predefined codes (\log and \sin in this case) which are simply displayed as normal, non-italicized text. For named operators that TeX has no code for, such as "cov" or "rank", use the \operatorname{} code. For example, try this: "r = \frac{ \operatorname{cov}_{xy} } { s_x s_y }".
$$ r = \frac{ \operatorname{cov}_{xy} } { s_x s_y } $$
Sometimes you need to put other words or letters in your equations that shouldn't be italicized because you don't want them to look like variables. In such instances you can use the \text{} code. For example, try this: "R = \pm \sqrt{ ( \frac{\text{Wald} - (2 \times df)}{-\text{LL}(\text{Original})} ) }".
$$ R = \pm \sqrt{ ( \frac{\text{Wald} - (2 \times df)}{-\text{LL}(\text{Original})} ) } $$
But, notice something wrong about that? How do we stretch those parentheses?
When you need left and right delimiters (such as parentheses, brackets,
and braces) to stretch vertically with their contents, use the
\left and \right codes before the opening
and closing delimiters. For example, in the last equation, put \left just
before the ( and \right just before the ), like this:
"R = \pm \sqrt{ \left( \frac{\text{Wald}-(2 \times df)}{-\text{LL}(\text{Original})} \right) }"
$$ R = \pm \sqrt{ \left( \frac{\text{Wald}-(2 \times df)}{-\text{LL}(\text{Original})} \right) } $$
If you need parentheses ( ) or square brackets [ ] you can type them directly from your keyboard. Other delimiters must be specified with a code.
| \(\lbrace \; \rbrace\) | \lbrace \rbrace | \(\langle \; \rangle\) | \langle \rangle | \(\lmoustache \; \rmoustache\) | \lmoustache \rmoustache |
| \(\lvert \; \rvert\) | \lvert \rvert | \(\lceil \; \rceil\) | \lceil \rceil | \(\lgroup \; \rgroup\) | \lgroup \rgroup |
| \(\lVert \; \rVert\) | \lVert \rVert | \(\lfloor \; \rfloor\) | \lfloor \rfloor |
All of those are extensible delimiters, meaning they can all be preceeded by the \left and \right codes to make them stretch vertically with their content. Give some of them a try.
When TeX renders fractions inside of other fractions it typically makes the inner fraction slightly smaller, which is a good thing. But if you need to have many fractions within fractions, you might not want them to keep getting smaller. To keep TeX from reducing the size, use the continuing fraction code, \cfrac, instead of \frac. For example, try typesetting this to see what it looks like: "\frac{1}{\sqrt{2} + \frac{1}{\sqrt{2} + \frac{1}{\sqrt{2}+\dotsb} } }". Then change each of those \frac codes to \cfrac to see the difference.
Finally, let's look at how you would show multiple-lines in an equation. This would be useful, for example, when you're writing instructional materials for a class and you want to show how to calculate a particular value. Here's an example. In the next step I'll show you how to do it.
\begin{align} \hat \sigma _ {\bar x} &= s / \sqrt{n} \\ &= 3.853 / \sqrt{250} \\ &= 3.853 / 15.811 \\ &= 0.244 \end{align}TeX uses ampersands & to set alignment points. So, to set the alignment points before the equals signs you put an ampersands in front of them. Typing new lines has no effect on TeX, it will ignore them just as it ignores spaces. Instead, TeX recognizes two backslashes \\ to indicate a newline. So to typeset the previous example, use this:
\hat \sigma _ {\bar x}
&= s / \sqrt{n} \\
&= 3.853 / \sqrt{250} \\
&= 3.853 / 15.811 \\
&= 0.244
That's it. We've covered the basics. To learn what else you can do with equations using TeX, peruse Michael Downes's excellent Short Math Guide for LaTeX. In the remaining steps I'll present you with some sample equations. Try to typeset them as best you can, then click the "See Answer" link under the equation to see the code that produced it. Have Downes's article open in a separate window as a reference for the codes. Just take them one small chunk at a time and go ahead and hit the "TYPESET IT" after each chunk. If it displays the codes instead of the equation, then you have something wrong (probably missed a closing brace).
$$ \bar x \pm t \frac{s}{\sqrt{n}} $$
$$ \bar x \pm t_{.005} (\hat \sigma_\bar x ) $$
$$ \bar x = \frac{\sum x_i}{n} $$
$$ \mu_{M_d}^2 = \frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2} $$
$$ n! \approx \sqrt{2 \pi n} \left( \frac{n}{e} \right) ^n $$
$$ \sigma_{p_1 - p_2} = \sqrt{ \frac{\pi_1 (1 - \pi_1)}{n_1} + \frac{\pi_2 (1 - \pi_2)}{n_2} } $$
$$ \operatorname{Pr} [Y = j] \; = \; _n C_j p^j (1-p)^{n-j} \quad (0 \leq j \leq n) $$
$$ \operatorname{Pr}[r] = \frac{N!}{r!(N - r)!} \pi^r (1 - \pi)^{N-r} $$
Confusion with braces will be the source of much of your mistakes and frustration. Problems will occur if you forget to close a brace that you've opened, or if you put the closing brace in the wrong place. If you get a strange error, or things don't look right, check your brace pairs. Try typesetting the following equation and see if you can get it to look right:
$$ \sigma_L = \sqrt{ \frac{\sum a_i^2}{n} \sigma_2 2 } $$
And now, for a final challenge, try this whopper!
$$ r = \frac{ \sum XY - \frac{\sum X \sum Y}{N} }{ \sqrt{ \left( \sum X^2 - \frac{(\sum X)^2}{N} \right) \left( \sum Y^2 - \frac {(\sum Y)^2}{N} \right) 2 } } $$
With MathJax you can put equations on your Web pages that look beautiful in any decent browser. I can't heap enough praise on the developers who produced MathJax. It is truly a thing of beauty.
To use MathJax on a Web page, simply add this single line to the <head> section of the page:
<script type="text/javascript"
src="http://cdn.mathjax.org/mathjax/latest/MathJax.js?config=TeX-AMS_HTML-full">
</script>
That's it. That's all you have to do. Once that's in place, adding an equation anywhere in your page is as simple as typing the TeX markup inside the standard TeX delimiters: $$ ... $$. So, for example, to place the equation for standard deviation onto the page, put the following on its own line in your HTMl file, as if it were a separate paragraph:
$$ s = \sqrt{\frac{ \sum (x_{i} - \bar{x})^2}{n - 1}} $$
That line in your HTML will end up being rendered by MathJax as this:
$$ s = \sqrt{\frac{ \sum (x_{i} - \bar{x})^2}{n - 1}} $$Using the standard $$ delimiters always puts the equation in its own paragraph. If you need an equation inline within the text of a paragraph you can use the standard TeX inline delimiters: \( ... \). For example, you might be talking about a linear model and want to show the equation in the text, like this: \( y = \alpha + \beta x + \epsilon \). You do that by simply typing it like this: \( y = \alpha + \beta x + \epsilon \).
To insert multi-line equations you can't use the $$ delimiters. Instead, you begin the lines with "\begin{align}" and end them with "\end{align}".
\begin{align}
\hat \sigma _ {\bar x}
&= s / \sqrt{n} \\
&= 3.853 / \sqrt{250} \\
&= 3.853 / 15.811 \\
&= 0.244
\end{align}
That code, in the middle of your HTML, will be picked up by MathJax and it will render it as follows:
\begin{aligned} \hat \sigma _ {\bar x} &= s / \sqrt{n} \\ &= 3.853 / \sqrt{250} \\ &= 3.853 / 15.811 \\ &= 0.244 \end{aligned}That's all there it to it. How simple is that? It's absolutely amazing. MathJax just totally rocks!
Here's another cool thing that's just icing on the cake. Notice how equations are a little difficult to read in the low-resolution of a web page, especially the superscripts and subscripts? Well, MathJax can allow the viewer to zoom the equation so it can be seen more clearly. Just move the mouse cursor over any equation and let it hover there for a couple of seconds and it will show it to you magnified! Go ahead. Try it. Hover over any equation on this page. They look beautiful. It's brilliant. (You can also set it to zoom by double-clicking instead of hovering.) To set your page so that it zooms on hover, add the following code to the <head> section of your Web page before the <script> tag that calls the MathJax script:
<script type="text/x-mathjax-config">
MathJax.Hub.Config({
menuSettings: { zoom: 'Hover' }
});
</script>
See this page for more information about configuring MathJax, and this page for all the configuration options.
Equations can be placed into any application by turning them into graphics files that can be pasted or imported. The ideal image format for equations is PDF, which can be placed within any application that can handle the PDF format. If your application can't handle PDF, then PNG is the next best alternative, but you'll need to PNG file to be a fairly high resolution, like 300 dots-per-inch, otherwise it won't print well and might not even be legible on-screen.
Mac OS X users can download the awesome LaTeXiT app, which allows you to typeset your equations in a window very similar to the tutorial above and then copy and paste them as PDFs or PNGs into your applications.
The first thing you need to do is download and install MacTeX. After you get that installed, reboot your Mac to make sure everything is in place. Next, download and install LaTeXiT.
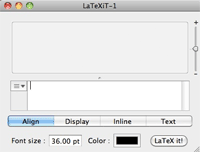
Figure 2: LaTeXiT Window
The LaTeXiT window is similar to the tutorial above, with a big output window at the top and a text input box at the bottom (see Figure 2). Strangely, LaTeXiT defaults to typesetting your equations in 36 pt type. I don't know why you would want them to be so huge, but there it is. The first thing you should do is change that to 12 pt. Leave the color black, and leave the mode on "Align" (I'll explain that later).
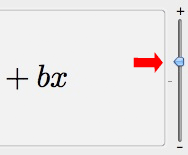
Figure 3: LaTeXiT Zoom Control
Now type something simple into the input box like "y = a + bx" (without the quotes), then click the "LaTeX it!" button. Your equation should appear in the top half of the window. Notice, however, that it's awfully small (assuming you changed the font size to 12 pt). To see it better LaTeXiT provides a magnification feature. Just drag the zoom controller up a little bit to zoom in on it (see Figure 3). From this point on you can just use LaTeXiT the same way you used the tutorial above. Remember, you don't have to type out the code for the entire equation at once. You can type small chunks of it at a time and click the "LaTeX it!" button as many times as you need to make sure it's looking correct.
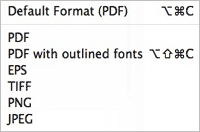
Figure 4: LaTeXiT Copy Menu
Now comes the cool part. When you're equation looks the way you want it to, right-click on it (or hold the CTRL key while you click, if you don't have a multi-button mouse—which you should) and you'll get to the menu shown in Figure 5. Notice the default is already set to PDF. This is ideal. The PDF format can be placed into just about any application on the Mac, and it can be resized to any size you need and will always look perfect, whether on screen or printed. You should always try to use PDF instead of PNG, JPEG, or GIF if at all possible.
You don't, however, have to go through the copy menu. For most applications all you have to do is drag your equation from the LaTeXiT window right onto the page of your Pages, Word, or PowerPoint file! How awesome is that? You can also use the copy and paste keyboard commands. At any time you can just hold down the Command and Option keys and hit the C key to copy the equation in PDF format to the clipboard. Once you have it in the clip board you can paste it into Pages, Word, PowerPoint, InDesign, Illustrator, or just about any other app (sadly, however, not OpenOffice or NeoOffice).
Unfortunately, for Windows users the situation isn't nearly so sweet. There's nothing anywhere close to as nice as LaTeXiT, and nothing that I've found that will produce the equations in PDF format.
Honestly, if you use Windows and you want to produce really good looking equations for your papers or presentations (that is, you want PDF), I would suggest just using the CodeCogs online Equation Editor. It will allow you to typeset equations using TeX markup, and then to download the equations in PDF format. It even has GUI menus for all the TeX codes, which is something LaTeXiT could use.
The best you can do for a Windows-native application is the LaTeX Equation Editor. It's clunky, and it only produces PNG files, but it will at least produce high-resolution PNG files, so that they'll look halfway decent in print.
First you need to download and install MiKTeX, the LaTeX distribution for Windows. During installation, leave the default setting of "Anyone who uses this computer." When it asks you where to install, put "C:\MiKTeX". And when it asks for "Prefered paper," if you're in the US change "A4" to "Letter." MiKTeX might install without a hitch, or it might not install at all, completely crapping out with a lovely error like this: "Windows API error 2: The system cannot find the file specified." It's hit or miss depending on your installation of Windows. I've had both experiences on Windows machines that were both running Windows XP SP3. Go figure.
After (and if ) you get MiKTeX installed, download and install LaTeX Equation Editor. The first time you run LaTeX Equation Editor you'll need to click on the "Settings" tab and tell it where to find the MikTeX "texify.exe" and "dvipng.exe" programs. If you installed it into C:\MikTeX, then you'll find both of them in "C:\MikTeX\miktex\bin\". If you installed it into C:\Program Files\MikTeX the they'll be in "C:\Program Files\MikTeX\miktex\bin".
Strangly, this program has no menus and no "Quit" button. To quit out of it, you're only option is to click the close-window button [X] in the top right of the window. As I said, it's clunky.
Sadly, there's no decent TeX equation editor (that I'm aware of) for Linux. There once was a very good one called Ekee that could even produce the equations in PDF format. But it has not been maintained for many years and apparently does not run on most newer versions of Linux. But, as I mentioned just above, you can use the CodeCogs online Equation Editor.
I hope this helped get you started with typesetting your own equations. To continue, you really need to read Downes's Short Math Guide for LaTeX. (You can skip sections 1 and 2 unless you want to learn about putting equations into LaTeX documents.) That will show you how to do more complicated things. If you're interested in learning how to typeset entire articles with LaTeX, you can go to Tobias Oetiker's Not So Short Introduction to LaTeX2e. And one more cool resource: if you know the symbol you need, and you can't find the TeX code for it, go to the Detexify site, draw the symbol and it will look up the code for you!
Chatelier, Pierre. LaTeXiT: A TeX Equation Editor for Mac. http://pierre.chachatelier.fr/programmation/latexit_en.php.
Bateman, Will. Online LaTeX Equation Editor. CodeCogs Engineering. (A very cool online TeX equation rendering engine that can produce many file formats including PNG, PDF, and even SVG.) http://www.codecogs.com/latex/about.php.
Downes, Michael. 2002. Short Math Guide for LaTeX. Providence, RI: American Mathematical Society. ftp://ftp.ams.org/pub/tex/doc/amsmath/short-math-guide.pdf.
MathJax. MathJax: Beautiful Math in All Browsers. http://www.mathjax.org/.
Oetiker, Tobias. 2011. The Not So Short Introduction to LaTeX2e: Or LaTeX2e in 174 Minutes. http://www.ctan.org/tex-archive/info/lshort/english/.
Pakin, Scott. 2009. The Comprehensive LaTeX Symbol List. The Comprehensive TeX Archive Network. http://mirrors.ctan.org/info/symbols/comprehensive/symbols-letter.pdf.
TeX Users Group. MacTeX: The Reference Edition of TeX for Mac. http://www.tug.org/mactex/.
Thrysoee, Jess. Laeqed - LaTeX Equation Editor. A Java-based app that runs on all operating systems, but only produces PNG format. http://www.thrysoee.dk/laeqed/.